MAKE A MEME
View Large Image
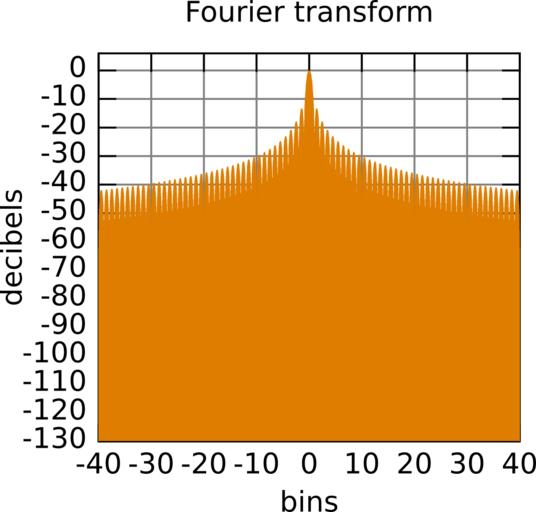
| View Original: | Fourier transform – Rectangular.svg (576x288) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Fourier transform – Rectangular.svg Fourier transform Rectangular window Trasformata di Fourier Finestra rettangolare own 2016-06-11 Bob K original version Olli Niemitalo BobQQ Luca Ghio cc-zero File Window function and frequency response - Rectangular svg Window function and its Fourier transform File Window function � Rectangular svg Window function Octave script The script below generates these SVG images File Window function and frequency response - Bartlett-Hann svg File Window function and frequency response - Blackman svg File Window function and frequency response - Blackman-Harris svg File Window function and frequency response - Blackman-Nuttall svg File Window function and frequency response - Approximate confined Gaussian sigma t 0 1N svg File Window function and frequency response - Confined Gaussian sigma t 0 1N svg File Window function and frequency response - Cosine svg File Window function and frequency response - Dolph-Chebyshev alpha 5 svg File Window function and frequency response - DPSS alpha 2 svg File Window function and frequency response - DPSS alpha 3 svg File Window function and frequency response - Exponential 60dB decay svg File Window function and frequency response - Exponential half window decay svg File Window function and frequency response - Gaussian sigma 0 4 svg File Window function and frequency response - Hamming alpha 0 53836 svg File Window function and frequency response - Hann svg File Window function and frequency response - Hann-Poisson alpha 2 svg File Window function and frequency response - Kaiser alpha 2 svg File Window function and frequency response - Kaiser alpha 3 svg File Window function and frequency response - Lanczos svg File Window function and frequency response - Nuttall continuous first derivative svg File Window function and frequency response - Parzen svg File Window function and frequency response - Planck-Bessel epsilon 0 1 alpha 4 45 svg File Window function and frequency response - Planck-taper epsilon 0 1 svg File Window function and frequency response - Rectangular svg File Window function and frequency response - SRS flat top svg File Window function and frequency response - Triangular svg File Window function and frequency response - Tukey alpha 0 5 svg File Window function and frequency response - Welch svg The script is not MATLAB-compatible <source lang matlab > pkg load signal graphics_toolkit gnuplot set 0 defaultaxesfontname sans-serif set 0 defaultaxesfontsize 12 set 0 defaultaxeslinewidth 1 function plotWindow w wname wfilename wspecifier wfilespecifier M 32; Fourier transform size as multiple of window length Q 512; Number of samples in time domain plot P 40; Maximum bin index drawn dr 130; Maximum attenuation dB drawn in frequency domain plot N length w ; B N sum w 2 /sum w 2 noise bandwidth bins k 0 1/Q 1; w2 interp1 0 1/ N-1 1 w k ; if M/N < Q Q M/N; endif figure 'position' 1 1 1200 600 subplot 1 2 1 area k w2 'FaceColor' 0 0 4 0 6 'edgecolor' 0 0 0 'linewidth' 1 if min w > -0 01 ylim 0 1 05 set gca 'YTick' 0 0 1 1 else ylim -1 5 set gca 'YTick' -1 1 5 endif ylabel 'amplitude' set gca 'XTick' 0 1/8 1 set gca 'XTickLabel' ' 0'; ' '; ' '; ' '; ' '; ' '; ' '; ' '; 'N-1' grid 'on' set gca 'gridlinestyle' '-' xlabel 'samples' if strcmp wspecifier title cstrcat wname ' window' 'interpreter' 'none' else title cstrcat wname ' window ' wspecifier ' ' 'interpreter' 'none' endif set gca 'Position' 0 094 0 17 0 38 0 71 H abs fft w zeros 1 M-1 N ; H fftshift H ; H H/max H ; H 20 log10 H ; H max -dr H ; k 1 M N-1-M N/2 /M; k2 -P 1/M P; H2 interp1 k H k2 ; subplot 1 2 2 set gca 'FontSize' 28 h stem k2 H2 '-' ; set h 'BaseValue' -dr xlim -P P ylim -dr 6 set gca 'YTick' 0 -10 -dr set findobj 'Type' 'line' 'Marker' 'none' 'Color' 0 8710 0 49 0 grid 'on' set findobj 'Type' 'gridline' 'Color' 871 49 0 set gca 'gridlinestyle' '-' ylabel 'decibels' xlabel 'bins' title 'Fourier transform' set gca 'Position' 0 595 0 17 0 385 0 71 if strcmp wfilename wfilename wname; endif if strcmp wfilespecifier wfilespecifier wspecifier; endif if strcmp wfilespecifier savetoname cstrcat 'Window function and frequency response - ' wfilename ' svg' ; else savetoname cstrcat 'Window function and frequency response - ' wfilename ' ' wfilespecifier ' svg' ; endif print savetoname '-dsvg' '-S1200 600' close endfunction N 2 17; Window length B is equal for Triangular and Bartlett from 2 17 k 0 N-1; s 0 1 N; w exp - k - N - 1 /2 2 / 4 s 2 - exp - -1/2 - N - 1 /2 2 / 4 s 2 exp - k+N - N - 1 /2 2 / 4 s 2 + exp - k-N - N - 1 /2 2 / 4 s 2 / exp - -1/2+N - N - 1 /2 2 / 4 s 2 + exp - -1/2 - N - N - 1 /2 2 / 4 s 2 ; plotWindow w App conf Gaussian Approximate confined Gaussian ' 0 1N' sigma_t 0 1N ; w parzenwin N '; plotWindow w Parzen ; w 1- k- N-1 /2 / N+1 /2 2; plotWindow w Welch ; alpha 5; Attenuation in 20 dB units w chebwin N alpha 20 '; plotWindow w Dolph Chebyshev Dolph-Chebyshev ' 5' alpha 5 w 0 35875 - 0 48829 cos 2 pi k/ N-1 + 0 14128 cos 4 pi k/ N-1 -0 01168 cos 6 pi k/ N-1 ; plotWindow w Blackman Harris Blackman-Harris w 0 62 -0 48 abs k/ N-1 -0 5 +0 38 cos 2 pi k/ N-1 -0 5 ; plotWindow w Bartlett Hann Bartlett-Hann w 0 53836 - 0 46164 cos 2 pi k/ N-1 ; plotWindow w Hamming Hamming ' 0 53836' alpha 0 53836 w 1 - 1 93 cos 2 pi k/ N-1 + 1 29 cos 4 pi k/ N-1 -0 388 cos 6 pi k/ N-1 +0 028 cos 8 pi k/ N-1 ; plotWindow w SRS flat top alpha 2; w 1/2 1 - cos 2 pi k/ N-1 exp alpha abs N-2 k-1 / 1-N ; plotWindow w Hann Poisson Hann-Poisson ' 2' alpha 2 w 0 42 - 0 5 cos 2 pi k/ N-1 + 0 08 cos 4 pi k/ N-1 ; plotWindow w Blackman w 0 355768 - 0 487396 cos 2 pi k/ N-1 + 0 144232 cos 4 pi k/ N-1 -0 012604 cos 6 pi k/ N-1 ; plotWindow w Nuttall Nuttall continuous first derivative w ones 1 N ; plotWindow w Rectangular w N/2 - abs k- N-1 /2 / N/2 ; plotWindow w Triangular w 0 5 - 0 5 cos 2 pi k/ N-1 ; plotWindow w Hann alpha 0 5; w ones 1 N ; n - N-1 /2 -alpha N/2; L length n ; w 1 L 0 5 1+cos pi abs n -alpha N/2 / 1-alpha N/2 ; w N -1 N-L+1 w 1 L ; plotWindow w Tukey Tukey ' 0 5' alpha 0 5 w sin pi k/ N-1 ; plotWindow w Cosine w sinc 2 k/ N-1 -1 ; plotWindow w Lanczos w N-1 /2 - abs 0 N-1- N-1 /2 / N-1 /2 ; plotWindow w Bartlett sigma 0 4; w exp -0 5 k- N-1 /2 / sigma N-1 /2 2 ; plotWindow w Gaussian Gaussian ' 0 4' sigma 0 4 alpha 2; w besseli 0 pi alpha sqrt 1- 2 k/ N-1 -1 2 /besseli 0 pi alpha ; plotWindow w Kaiser Kaiser ' 2' alpha 2 alpha 3; w besseli 0 pi alpha sqrt 1- 2 k/ N-1 -1 2 /besseli 0 pi alpha ; plotWindow w Kaiser Kaiser ' 3' alpha 3 tau N-1; epsilon 0 1; t_cut tau 0 5 - epsilon ; T_in abs k - 0 5 tau ; z_exp t_cut - 0 5 tau / T_in - t_cut + t_cut - 0 5 tau / T_in - 0 5 tau ; sigma T_in < 0 5 tau / exp z_exp + 1 ; w 1 T_in < t_cut + sigma T_in > t_cut ; plotWindow w Planck-taper Planck-taper ' 0 1' epsilon 0 1 w 0 3635819 - 0 4891775 cos 2 pi k/ N-1 + 0 1365995 cos 4 pi k/ N-1 -0 0106411 cos 6 pi k/ N-1 ; plotWindow w Blackman Nuttall Blackman-Nuttall tau N/2 ; w exp -abs k- N-1 /2 /tau ; plotWindow w Exponential Exponential ' N/2' half window decay tau N/2 / 60/8 69 ; w exp -abs k- N-1 /2 /tau ; plotWindow w Exponential Exponential ' N/2 / 60/8 69 ' 60dB decay tau N-1; alpha 4 45; epsilon 0 1; t_cut tau 0 5 - epsilon ; t_in k - 0 5 tau; T_in abs t_in ; z_exp t_cut - 0 5 tau / T_in - t_cut + t_cut - 0 5 tau / T_in - 0 5 tau ; sigma T_in < 0 5 tau / exp z_exp + 1 ; w 1 T_in < t_cut + sigma T_in > t_cut besseli 0 pi alpha sqrt 1 - 2 t_in / tau 2 / besseli 0 pi alpha ; plotWindow w Planck Bessel Planck-Bessel 0 1 4 45 epsilon 0 1 alpha 4 45 N 4097; k 0 N-1; alpha 2; s sin alpha 2 pi/N 1 N-1 /1 N-1; c0 alpha 2 pi/N s; A toeplitz c0 ; V evals eigs A 1 ; emax imax max abs diag evals ; w abs V imax ; w w '; w w / max w ; plotWindow w DPSS DPSS ' 2' alpha 2 N 4097; k 0 N-1; alpha 3; s sin alpha 2 pi/N 1 N-1 /1 N-1; c0 alpha 2 pi/N s; A toeplitz c0 ; V evals eigs A 1 ; emax imax max abs diag evals ; w abs V imax ; w w '; w w / max w ; plotWindow w DPSS DPSS ' 3' alpha 3 global N T P abar target_stnorm; N 2049; This is will take a lot of time with N 2049 k 0 N-1; target_stnorm 0 1; function g sigma_w sigma_t CGWn alpha n determine eigenvectors of M alpha global N P T opts maxit 10000; if n ~ N g lambda eigs P + alpha T n 'sa' opts ; else g lambda eig P + alpha T ; end sigma_t sqrt diag g' T g / g' g ; sigma_w sqrt diag g' P g / g' g ; end function h1 helperCGW anorm global N abar target_stnorm ~ ~ sigma_t CGWn anorm abar 1 ; h1 sigma_t - target_stnorm N; end define alphabar and matrices T and P T zeros N N ; P zeros N N ; for k 1 N T k k k - N+1 /2 2; for l 1 N if k ~ l P k l 2 -1 k-l / k-l 2; else P k l pi 2/3; end end end abar 10/N 4/4 anorm aval fzero helperCGW 0 1/target_stnorm ; CGWg CGWsigma_w CGWsigma_t CGWn anorm abar 1 ; w CGWg sign mean CGWg ; w w'/max w ; plotWindow w Confined Gaussian Confined Gaussian ' 0 1N' sigma_t 0 1N ; </source> The generated SVG files should be post-processed by the following Perl script to change the SVG metadata title from Gnuplot to the body of the file name and to unobfuscate Unicode character codes for Greek symbols and en dash The script will scan the current directory for svg files and makes the necessary changes if they have not already been made <source lang perl > /usr/bin/perl opendir DIR ' ' or die ; while file readdir DIR ext substr file length file -4 ; if ext eq ' svg' print file\n ; pre name split - substr file 0 length file -4 ; lines ; open INPUTFILE < file or die ; while line <INPUTFILE> line ~ s/ / /g; if line eq <title>Gnuplot</title>\n line '<title>Window function and its Fourier transform ' name </title> \n ; lines0+ lines line; close INPUTFILE ; open OUTPUTFILE > file or die ; for t 0; t < lines; t++ print OUTPUTFILE lines t ; close OUTPUTFILE ; closedir DIR ; </source> Window function Images with Octave source code Images with Perl source code | ||||