MAKE A MEME
View Large Image
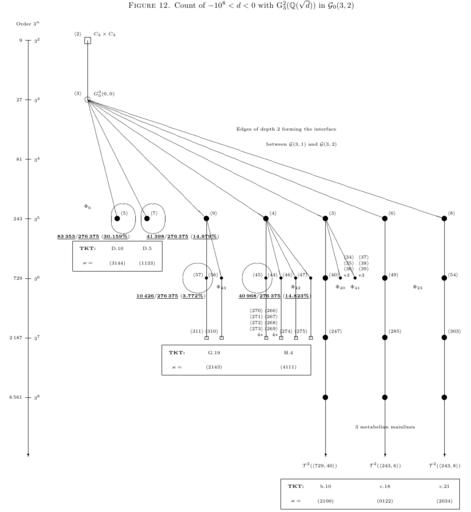
| View Original: | FrequencyCoclass2Type33Sporadic.tiff (1093x1188) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: FrequencyCoclass2Type33Sporadic.tiff This diagram shows the interface between the graphs of finite 3-groups with coclass 1 and 2 and abelianization of type 3 3 Important vertices are labelled with their SmallGroups Library identifier in angle brackets The vertices 5 7 57 and 45 are most densely populated by second 3-class groups of complex quadratic fields with discriminant in the range -10 8<d<0 The underlined counters adjacent to the ovals surrounding these vertices give the absolute and relative frequency of the distribution TKT means transfer kernel type <br/> User DanielConstantinMayer replaced the png file by a tiff file with higher resolution thereby adding more details and in particular supplementing two missing groups <2187 274> and <2187 275> Additionally two counters 83352 and 40967 had to be increased by 1 since a minor error occurred in the current version of the paper by Boston Bush and Hajir The distribution was computed by Michael R Bush WLU Lexington VA It is reproduced here with his permission provided his authorship is acknowledged with every usage of the information 2014-11-17 DanielConstantinMayer talk Uploads There exists a similar png file with identifier FrequencyCoclass2Type33Sporadic png which contains less information DanielConstantinMayer wikipedia en Cc-zero Original upload log en wikipedia FrequencyCoclass2Type33Sporadic tiff wikitable - 2014-11-17 14 11 1093×1188× 150562 bytes DanielConstantinMayer User DanielConstantinMayer replaced the png file by a tiff file with higher resolution thereby adding more details and in particular supplementing two missing groups <2187 274> and <2187 275> Additionally two counters 83352 and 40967 had to be i Uncategorized 2016 May 5 | ||||