MAKE A MEME
View Large Image
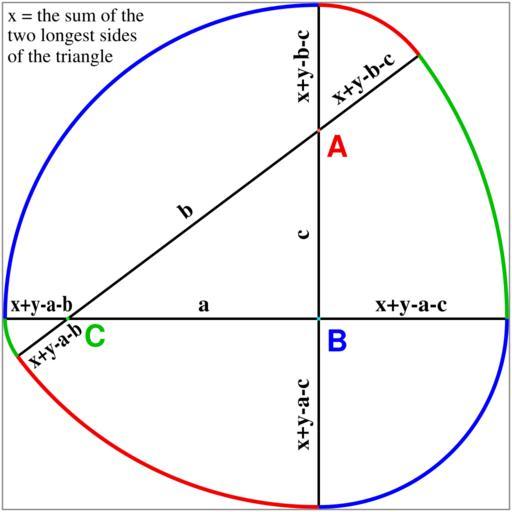
| View Original: | How to make mathematical roller curve based on triangle.svg (680x680) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: How to make mathematical roller curve based on triangle.svg Diagram showing how to construct a mathematical roller i e constant-width curve based on any triangle In the diagram A B C are the vertices of the triangle while a b c are the lengths of the opposing sides If x is defined as the sum of the lengths of the two longest sides of the triangle while y is an arbitrarily-chosen non-negative padding factor then the constant-width roller curve will be constructed from the following six circular arcs Radius x+y-a centered at A Radius x+y-b-c centered at A Radius x+y-b centered at B Radius x+y-a-c centered at B Radius x+y-c centered at C Radius x+y-a-b centered at C The arcs with two negative terms in the definition of the radius are on the same side of the triangle as the vertices at their centers while the arcs with one negative term in the definition of the radius are on the opposite side of the triangle The overall diameter of constant width of the curve is calculated as the sum of the lengths of the two longest sides of the triangle x plus twice the padding factor 2y minus the length of the shortest side of the triangle The perimeter is pi times the diameter as for a circle If the padding factor y is set at zero then at least one of the arcs will be of zero radius which means that there will be a point of tangent discontinuity where curves join at a vertex of the triangle In the case of an isoceles triangle where the equal angles are less than 60° y 0 means that there will two points of tangent discontinuity while in the case of an equilateral triangle there will be three points of tangent discontinuity i e a Reuleaux triangle In the diagram there is a Pythagorean triangle with sides of relative length 3 4 5 so x 9 while the padding factor is 1 unit i e y 1 This means that there will be circular arcs of radius 5 and 3 centered on the right angle vertex B in the diagram circular arcs of radius 7 and 1 centered on the vertex opposite the shortest side of the triangle C in the diagram and circular arcs of radius 6 and 2 centered on the other vertex A The overall constant diameter is 8 units and the perimeter sum of the length of the six arcs is 8Ď This can be seen from the following calculation proceeding counterclockwise from the top where 36 869898° atan 3/4 and angle is converted to arc length by multiplying it times radius times the radian conversion factor Ď /180 Degrees Radius Arc Length ----- --- ----------- 90 5 2 5pi 36 869898 1 0 20483276pi 53 130102 6 1 77100341pi 90 3 1 5pi 36 869898 7 1 43382935pi 53 130102 2 0 59033447pi ------- Total perimeter 8pi To see a diagram of a constant-width curve based on a 3 4 5 Pythagorean triangle with padding factor y 0 and so with five circular arcs and one tangent discontinuity point see image File Curve of constant width svg This diagram is based on information in the book Mathematical Models by H Martyn Cundy and A P Rollett second edition 1961 Oxford University Press p 211 combined with an adapted version of some of the layout details from PD diagram File Curve of constant width svg Generated from the following vector PostScript source code <pre> 300 396 translate/x 36 869897646 def 2 setlinewidth 150 0 moveto -250 0 lineto stroke 0 -150 moveto 0 250 lineto stroke -240 -30 moveto 80 210 lineto stroke 0 875 1 setrgbcolor 0 0 1 5 0 360 arc closepath fill 0 925 0 setrgbcolor -200 0 1 5 0 360 arc closepath fill 1 4 4 setrgbcolor 0 150 1 5 0 360 arc closepath fill 3 setlinewidth 0 0 8 setrgbcolor 0 0 250 90 180 arc stroke 0 0 150 270 360 arc stroke 0 75 0 setrgbcolor -200 0 50 180 dup x add arc stroke -200 0 350 0 x arc stroke 95 0 0 setrgbcolor 0 150 300 180 x add 270 arc stroke 0 150 100 x 90 arc stroke /Helvetica-bold 24 selectfont 6 129 moveto A show 0 0 8 setrgbcolor 6 -26 moveto B show 0 75 0 setrgbcolor -187 -22 moveto C show 0 setgray/Times-bold 18 selectfont -96 6 moveto a show 45 6 moveto x+y-a-c show gsave 90 rotate -105 8 moveto x+y-a-c show 63 8 moveto c show 172 8 moveto x+y-b-c show grestore gsave x rotate -38 127 moveto b show 114 127 moveto x+y-b-c show /Times-bold15 0 0 18 0 0selectfont -205 5 104 moveto x+y-a-b show grestore /Times-roman 15 selectfont -248 237 moveto x the sum of the show -248 221 25 moveto two longest sides show -248 204 5 moveto of the triangle show /Times-bold15 0 0 18 0 0selectfont -245 5 6 moveto x+y-a-b show 5 setgray 1 setlinewidth -252 252 moveto 404 0 rlineto 0 -404 rlineto -404 0 rlineto closepath stroke showpage EOF</pre> 2010-12 AnonMoos thumb center Curves of constant width Images with PostScript source code Triangle geometry | ||||