MAKE A MEME
View Large Image
| View Original: | Lotka-Volterra competition model, flow 3.png (1306x1311) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
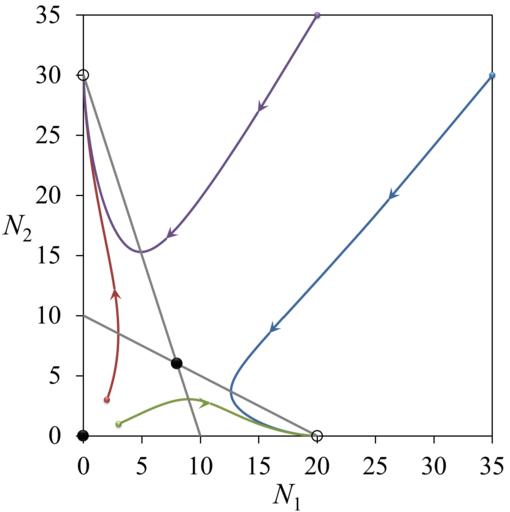
| Keywords: Lotka-Volterra competition model, flow 3.png K<sub>1</sub> <sub>12</sub> かつ K<sub>1</sub> > K<sub>2</sub> <sub>21</sub> のときの解曲線例 方程式は <math>\frac dN_1 dt r_1 N_1 \left 1-\frac N_1+\alpha_ 12 N_2 K_1 \right </math> <math>\frac d N_2 dt r_2 N_2 \left 1-\frac N_2+\alpha_ 21 N_1 K_2 \right </math> で 使用した各パラメータは r<sub>1</sub> 1 r<sub>2</sub> 1 5 K<sub>1</sub> 20 K<sub>2</sub> 30 <sub>12</sub> 2 <sub>21</sub> 3 各曲線の N<sub>1</sub> N<sub>2</sub> は 35 30 紫 20 35 赤 2 3 紫 3 1 解曲線の数 データは下のScilabを使用して得た 2016-09-04 own Yapparina other versions Scilab source <source lang scilab > clear; r1 1 r2 1 5 K1 20 K2 30 a12 2 a21 3 function dx LVc t x dx 1 r1 x 1 1- x 1 +a12 x 2 /K1 ; dx 2 r2 x 2 1- x 2 +a21 x 1 /K2 ; endfunction T linspace 0 10 100 ; x01 2 ; 3; x1 ode x01 0 T LVc ; x02 3 ; 1; x2 ode x02 0 T LVc ; x03 20 ; 35; x3 ode x03 0 T LVc ; x04 35 ; 30; x4 ode x04 0 T LVc ; csvWrite x1 ' 'flow1 csv' csvWrite x2 ' 'flow2 csv' csvWrite x3 ' 'flow3 csv' csvWrite x4 ' 'flow4 csv' </source> cc-zero Lotka Volterra competition model | ||||
