MAKE A MEME
View Large Image
| View Original: | Monty Hall problem game theory.png (998x685) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
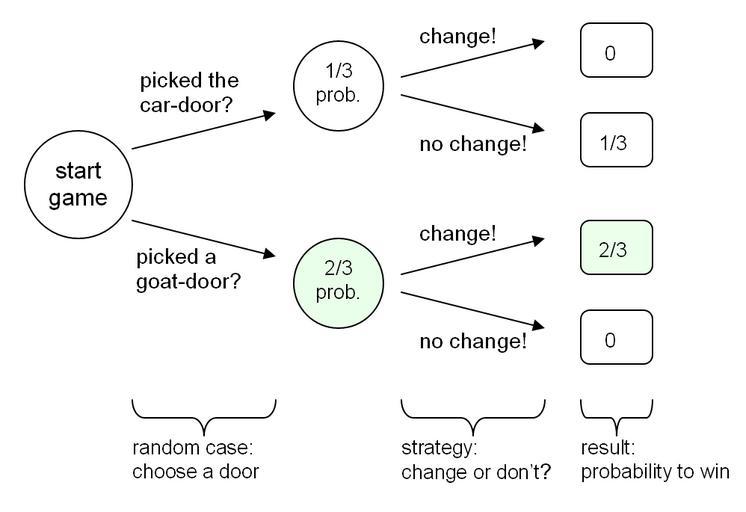
| Keywords: Monty Hall problem game theory.png The Monty Hall problem describes a game show with 3 doors Behind one door is a car and behind the other 2 doors are goats The probability of choosing the car-door at the start is 1/3 The probability of choosing a goat-door is 2/3 Note that there is no need to distingush between the two goat doors they are equal If you chose the car-door in the first try changing will definitely let you lose while not changing will definitely let you win the car If you chose a goat-door in the first try changing will definitely let you win while not changing will let you lose That is because the host reveals the other goat door to you and only the car-door remains to be picked It's better not to change in case 1 and it's better to change in case 2 As you don't known in which case you are and case 2 is more likely 2/3 prob you should always change That makes an overall-probability of 2/3 1 2/3 to win when you change while not changing gives you 1/3 1 1/3 chance to win Own 2008 Unify public domain diagram Game theory | ||||