MAKE A MEME
View Large Image
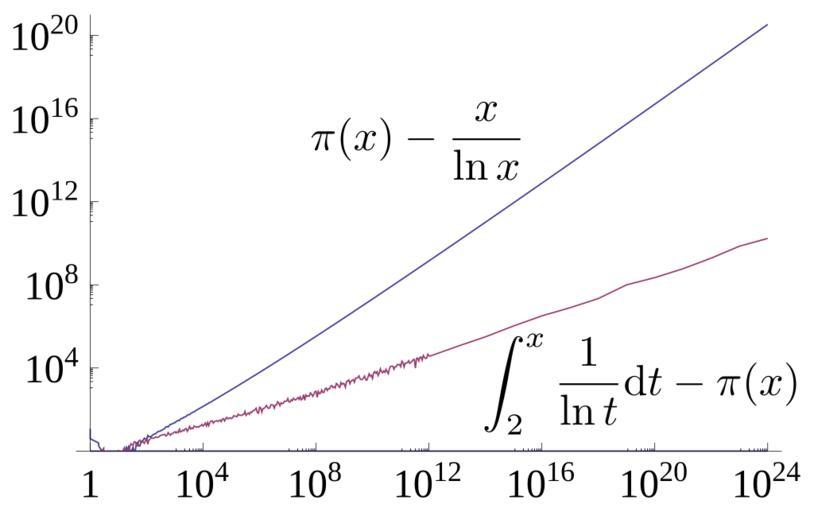
| View Original: | Prime number theorem absolute error.svg (282x177) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: Prime number theorem absolute error.svg en A log-log plot showing the absolute error of two estimates to the prime-counting function <math>\pi x </math> given by <math>\frac x \ln x </math> and <math>\int_2 x \frac 1 \ln t \mathrm d t Li x li x - li 2 </math> The x axis is <math>x</math> and is logarithmic labelled in evenly spaced powers of 10 going up to 10<sup>24</sup> the largest <math>x</math> for which <math>\pi x </math> is currently known The y axis is also logarithmic going up to the absolute error of <math>x/\ln x</math> at 10<sup>24</sup> The error of both functions appears to increase as a power of <math>x</math> with Li x 's power being smaller; both clearly diverge The error of Li x appears to smooth out after 10<sup>9</sup> but this is an artifact due to less data availability for <math>\pi x </math> in the larger region Source used to generate this chart is shown below own User Dcoetzee 2013-03-21 Prime numbers Cc-zero Source All source released under CC0 waiver Mathematica source to generate graph which was then saved as SVG from Mathematica <pre> base N10/600 ; diffs Tablebase x Nbase x - base x/ x Logbase x 1 Floor2 base ; diffsli Tablebase x Nbase x - LogIntegralbase x - LogIntegral2 x Ceilingbase 2 Floor2 base ; Supplement with larger known PrimePi values that are too large for \ Mathematica to compute LargePiPrime 10 13 346065536839 10 14 3204941750802 10 15 29844570422669 10 16 279238341033925 10 17 2623557157654233 10 18 24739954287740860 10 19 234057667276344607 10 20 2220819602560918840 10 21 21127269486018731928 10 22 201467286689315906290 10 23 1925320391606803968923 10 24 18435599767349200867866 ; diffs2 Abs1 N2 - 1/ Log1 LargePiPrime; diffsli2 Abs1 N2 - LogIntegral1 - LogIntegral2 LargePiPrime; Plot with log x axis together with the horizontal line y 1 Show1 x 1 10 24 PlotRange -> 1 10 21 ListLogLogPlot diffs2 diffsli2 Joined -> True PlotRange -> 1 10 21 LabelStyle -> FontSize -> 14 </pre> LaTeX source for labels <pre> \pi x - \frac x \ln x \int_2 x \frac 1 \ln t \mathrm d t - \pi x </pre> These were converted to SVG with http //www tlhiv org/ltxpreview/ and then the graph was embedded into the resulting document in Inkscape Axis fonts were also converted to Liberation Serif in Inkscape | ||||