MAKE A MEME
View Large Image
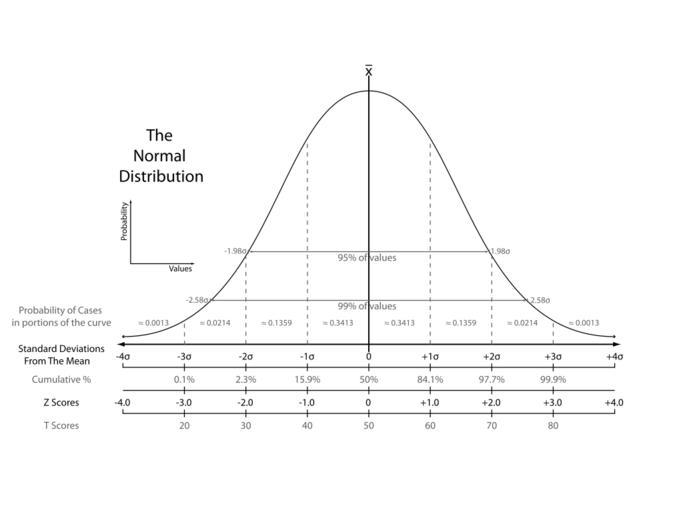
| View Original: | The Normal Distribution.svg (800x600) | |||
| Download: | Original | Medium | Small | Thumb |
| Courtesy of: | commons.wikimedia.org | More Like This | ||
| Keywords: The Normal Distribution.svg The re-drawn chart comparing the various grading methods in a normal distribution Includes Standard deviations cumulative percentages percentile equivalents Z-scores and T-scores Inspired by Figure 4 3 on Page 74 of Ward A W Murray-Ward M 1999 Assessment in the Classroom Belmont CA Wadsworth ISBN 0534527043<br /> Note The 95 range is labelled as -1 98 to +1 98 standard deviations This is probably a typographic error as the correct range is plus or minus 1 96 standard deviations en wikipedia Abdull 2007-07-12 Heds 1 wikipedia en Discussion What is the z-score which has the steepest points of the curve My guess it is z -1 +1 The way to tell is to differentiate the pdf and find its maxima but not sure if I'm up to that Is the 1 98 sigma/z-score for 95th percentile a typo 1 96 is nearer 95 than 1 98 which corresponds to 95 2269 Y axis stands not for probability as stated but rather for probability density Probability itself is zero for each given point I think this is the important point yes this plot is wrong Also another comment the Probability Probability Density cannot be negative -1 980 or -2 580 even though the X is negative If you want the probability within some interval you would calculate the integral from one endpoint to the other With the Normal Distribution there is no elementary anti-derivative so the values are calculated using numerical methods This is why you usually refer to a table that contains the calculated values In order to use the tables you must first calculate the z-score Heds 1 original upload log en wikipedia Abdull en wikipedia The+Normal+Distribution svg 2007-07-12 14 47 Heds 1 800×600×0 123727 bytes <nowiki>A re-drawn chart comparing the various grading methods in a normal distribution Includes Standard deviations cumulative percentages percentile equivalents Z-scores and T-scores Inspired by Figure 4 3 on Page 74 of Ward A W Murray-Ward M 1999 </nowiki> 2007-07-12 14 44 Heds 1 800×600×0 137472 bytes <nowiki>The re-drawn chart comparing the various grading methods in a normal distribution Includes Standard deviations cumulative percentages percentile equivalents Z-scores and T-scores Inspired by Figure 4 3 on Page 74 of Ward A W Murray-Ward M 199</nowiki> Normal distribution Economic statistics | ||||